Logarithms may seem tricky at first, but they're just a way to think about powers and exponents. Whether you need to understand logarithms for an exam, are brushing up on your algebra, or will be using them as part of another maths topic, you need to know how they work. Here, we'll break down the log rules, the key logarithm laws, and show you how and when to use them.

What Are Logarithms?
A logarithm is the inverse of an exponent. If you know that:
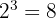
Then the corresponding logarithmic expression is:
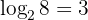
2 must be raised to the power of 3 to get 8. The logarithmic form of an exponential equation:
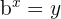
can be rewritten as:
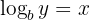
Where:
 is the base
is the base is the result
is the result is the exponent
is the exponent
Logarithms and exponents are inverse operations. While exponents tell you the result of raising a base to a power, logarithms tell you which power was used. Understanding this relationship is key to mastering both forms.
Logarithms are helpful because they enable us to work with very large or tiny numbers more easily. This allows us to solve equations where the unknown is in the exponent. Logarithms are a fundamental part of mathematics and are used in science, engineering, computer science, and finance.

Like basic arithmetic has rules for addition and multiplication, logarithms have their own set of log rules or logarithm rules, which make them easier to work with. Once you understand these, you'll be able to simplify expressions, solve equations, and feel more confident using logs in any tricky maths situations.
Here are logarithms explained quickly.
Why Learn Logarithms?
Like many maths students, when they come across a new topic or concept, they're probably asking themselves, "Why bother learning logarithms at all?"
You won't use logarithms when out shopping, but they're so key to many areas of maths, science, and technology that they're worth understanding. You can use them to model exponential growth and decay, which are observed in real-world systems such as population trends, radioactive decay, interest rates, and the Richter scale for earthquakes.

Logs are essential when you want to solve an equation where the unknown is in the exponent, which you can't do with introductory algebra. Studying logarithms also lays the groundwork for more advanced topics like differentiation and integration.
To solve an equation:
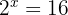
you need to rewrite it using a logarithm:
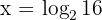
which simplifies to:

Logarithms are also essential to computer algorithms, machine learning, sound engineering, and even encryption systems. Sure, they can help you pass exams that include them, but they'll also help you understand the log laws that govern natural and technological systems.
Speaking of maths exams. Studying logarithms helps tackle several maths problems. When it comes to logarithmic functions, complex equations, and calculus, which you'll move onto later, logs are essential.
Logarithms aren’t just for exams; they’re used in earthquake measurement (Richter scale), sound intensity (decibels), population models, pH in chemistry, and finance (compound interest). Any time exponential change is involved, logs help us understand it.

Understanding the Basics of Logarithms
Before we look at log rules, let's see how logarithms work and how they relate to exponents.
A logarithm is the answer to the following question: To what power must the base be raised to produce a given number?
For example:
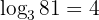
because:
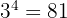
Logarithmic Notation
Logarithms are written in this general form:
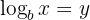
This means that:
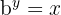
Here:

 is the value or result
is the value or result is the exponent (or power)
is the exponent (or power)
This expresses the same relationship in a different form.
Common Types of Logarithms
The two logarithms that you'll often come across in maths classes are:
Common logarithm — Base 10:
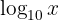
Often written simply as:
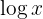
Natural logarithm — Base e, where e≈2.718e:
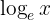
Usually written as:
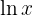
These are often used in science, economics, and engineering.
Exponentials and Their Inverses
A logarithmic function is the inverse of an exponential function. If:
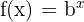
then its inverse is:
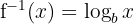
Reverse exponential processes using logs to solve certain types of equations.
The Core Logarithm Rules You Need to Know
Certain logarithm rules, also known as log laws, can be used to simplify and solve logarithmic expressions. Make sure you know these three core log rules.
1. Product Rule
The product rule allows you to break apart the log of a product into a sum of logs:
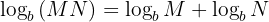
Example:
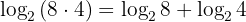

Use the product rule to make complex expressions much easier to manage especially when solving equations or simplifying logarithmic functions.
2. Quotient Rule
Deal with division inside a logarithm by turning it into a subtraction:
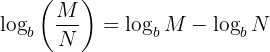
Example:
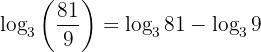
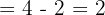
This is useful when simplifying expressions involving ratios or fractions.
3. Power Rule
You can move an exponent in the argument of a log out to the front as a multiplier:
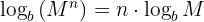
Example:
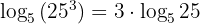
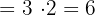
You can use this when solving logarithmic equations involving powers or exponents.
These three core rules, the product, quotient, and power, are key to most log simplification techniques. You can build on these logarithm rules to solve more complex problems and equations.
- Don’t apply log rules to addition inside a log.
- Always check that the log’s input is positive
- Don’t forget to simplify powers before applying rules
Additional Log Laws and Properties
After the three core rules, there are a few more essential log laws you can use when working with logarithms. These are typically reserved for exceptional cases, but they do provide some flexibility when solving certain equations.

Log of 1
Any logarithm of 1, regardless of the base, is always 0:
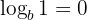
This is because any number raised to the power of 0 is 1:

For example:
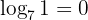
Log of the Base
When the base and the argument are the same, the result is always 1:
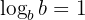
Example:
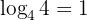
Because:
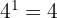
Change of Base Formula
Using this rule, you can rewrite logarithms in a different base. You can use this when you're using a calculator that only supports base 10 or base e:
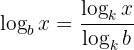
Example using base 10:
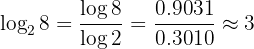
Logs with Negative or Zero Arguments
Logs are undefined for zero and negative numbers in the real number solution.
This means that there is no real solution to:
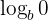
And:

is not defined unless you're working in complex numbers.
Before solving or simplifying, always verify that the input to a logarithm is positive.
With these additional logarithm rules, you can evaluate, transform, and solve a wider variety of problems. Any student of algebra can use them with the core rules to create a log laws toolkit that will get you out of most situations with logs.

These additional log laws give you flexibility when working across subjects from maths to physics. If you're diving into topics like maths mechanics, kinematics, forces, or energy, you'll see how logs help describe motion and change.
Solving Logarithmic Equations
Once you've got the hang of the log rules, you can start using them to solve equations that involve logarithms. Usually, you'll have to find the unknown value that makes the equation true by applying the log laws to simplify or isolate the variable. You'll either be dealing with equations with a single log or equations with a log on either side.
1. Equations with a Single Log
These kinds of equations are the easier of the two to solve. You have to isolate the logarithm and convert it to exponential form.
Example:
Solve
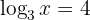
Step 1: Convert to exponential form:
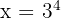
Step 2: Simplify:
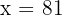
2. Equations with Logs on Both Sides
You can use the properties of logarithms to eliminate the logs and solve the algebraic equation you end up with.
Example:
Solve
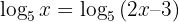
Step 1: Since the logs have the same base, drop the logs:
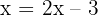
Step 2: Solve for x:
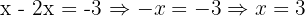
3. Equations that Require Log Rules
Apply the product, quotient, or power rule to combine or simplify terms.
Example:
Solve
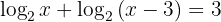
Step 1: Use the product rule:

Step 2: Convert to exponential form:
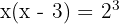
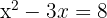
Step 3: Solve the quadratic:
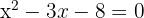
Use the quadratic formula:
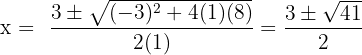
Only keep positive results that don't make the log undefined.
Tips for Solving Logarithmic Equations
- Remember that logs are only defined for positive arguments so always check for extraneous solutions.
- Use logarithmic identities to simplify before converting to exponential form.
- If you’re stuck, try taking the logarithm of both sides using base 10 or base e.
students across New Zealand study logarithms as part of the NCEA Level 2 and Level 3 maths curriculum.
If you need help with logarithms or any other type of maths, like calculus, look for help with a private maths tutor. On Superprof, you can find maths tutors all over New Zealand and around the world. With most offering the first session for free, you can even try a few before choosing the one that suits you and your learning style. Just search for maths on the Superprof site today!
Résumer avec l'IA :















